Der ID3 (Iterative Dichotomiser 3)-Algorithmus ist ein grundlegender Algorithmus zur Konstruktion von Entscheidungsbäumen, die häufig in der maschinellen Lernwelt verwendet werden, und wurde von Ross Quinlan entwickelt. Es ist ein greedy Algorithmus, der den Datenraum rekursiv in Unterräume unterteilt, indem er bei jedem Schritt das Attribut auswählt, das den größten Informationsgewinn bietet. Diese Methode sorgt dafür, dass die Daten in eine logische Struktur gebracht werden, die zur Lösung des Klassifikationsproblems führt.
Funktionsweise von ID3
Der ID3-Algorithmus verwendet ein Kriterium namens Informationsgewinn, um zu entscheiden, welches Attribut am besten geeignet ist, die Daten zu teilen. Dazu wird der Entropie-Begriff aus der Informationstheorie verwendet, um die Reinheit einer Datenmenge zu messen. Je reiner eine Datenmenge, desto näher ist ihre Entropie bei Null.
Die Schritte des ID3-Algorithmus lauten:
- Wähle das Attribut mit dem höchsten Informationsgewinn.
- Teile den Datensatz basierend auf dem Wert des ausgewählten Attributs auf.
- Wiederhole den Prozess rekursiv, bis alle Attribute verwendet wurden oder der Baum die maximale Tiefe erreicht hat.
Die Mathematik des ID3-Algorithmus
Um den ID3-Algorithmus vollständig zu verstehen, müssen wir die mathematischen Konzepte der Entropie und des Informationsgewinns untersuchen. Diese Konzepte helfen uns, die Güte einer Attributteilung zu bewerten.
1. Entropie
Die Entropie misst die Unordnung oder Unsicherheit in einer Menge. Wenn eine Datenmenge nur eine Klasse enthält (z. B. nur “positiv”), dann ist die Entropie 0. Wenn die Daten gleichmäßig auf verschiedene Klassen verteilt sind, ist die Entropie maximal.
Die Entropie \( H(S) \) eines Datensatzes \( S \), der in Klassen unterteilt ist, wird durch die folgende Formel definiert:
\[
H(S) = – \sum_{i=1}^{k} p_i \log_2(p_i)
\]
wobei:
– \( p_i \) der Anteil der Elemente im Datensatz \( S \) ist, die zur Klasse \( i \) gehören,
– \( k \) die Anzahl der Klassen ist.
Ein Beispiel: Wenn wir einen Datensatz mit 14 Einträgen haben, die aus 9 positiven und 5 negativen Beispielen bestehen, wäre die Entropie:
\[
H(S) = -\left( \frac{9}{14} \log_2 \frac{9}{14} + \frac{5}{14} \log_2 \frac{5}{14} \right) = 0.940
\]
2. Informationsgewinn
Der Informationsgewinn gibt an, wie viel Unsicherheit durch das Hinzufügen eines Attributs verringert wird. Er wird berechnet als die Differenz zwischen der Entropie des ursprünglichen Datensatzes und der gewichteten Entropie der durch das Attribut erzeugten Teilmengen.
Sei \( A \) ein Attribut mit \( v \) möglichen Werten, dann ist der Informationsgewinn \( \text{Gain}(S, A) \) definiert als:
\[
\text{Gain}(S, A) = H(S) – \sum_{i=1}^{v} \frac{|S_i|}{|S|} H(S_i)
\]
wobei:
– \( S_i \) die Teilmenge von \( S \) ist, bei der das Attribut \( A \) den Wert \( i \) hat,
– \( |S_i| \) die Anzahl der Elemente in der Teilmenge \( S_i \),
– \( H(S_i) \) die Entropie dieser Teilmenge ist.
Der ID3-Algorithmus wählt bei jedem Schritt das Attribut, das den höchsten Informationsgewinn hat, und wiederholt den Prozess, bis alle Attribute verarbeitet wurden oder die Teilmengen vollständig klassifiziert sind.
Beispiel: Ein Entscheidungsbaum mit ID3
Um die Funktionsweise von ID3 zu verdeutlichen, betrachten wir ein einfaches Beispiel zur Wettervorhersage. Wir haben einen Datensatz mit den folgenden Attributen: Wetterlage (sonnig, regnerisch, bewölkt), Wind (ja, nein), und wir wollen klassifizieren, ob man Federball spielen kann (ja/nein):| Wetterlage | Wind | Federball spielen | |
|---|---|---|---|
| 0 | sonnig | nein | ja |
| 1 | sonnig | nein | ja |
| 2 | sonnig | ja | ja |
| 3 | bewölkt | nein | ja |
| 4 | bewölkt | nein | ja |
| 5 | bewölkt | ja | ja |
| 6 | regnerisch | nein | nein |
| 7 | regnerisch | ja | nein |
| 8 | regnerisch | ja | nein |
| 9 | sonnig | nein | ja |
| 10 | sonnig | ja | nein |
| 11 | bewölkt | ja | ja |
| 12 | regnerisch | nein | nein |
| 13 | bewölkt | nein | ja |
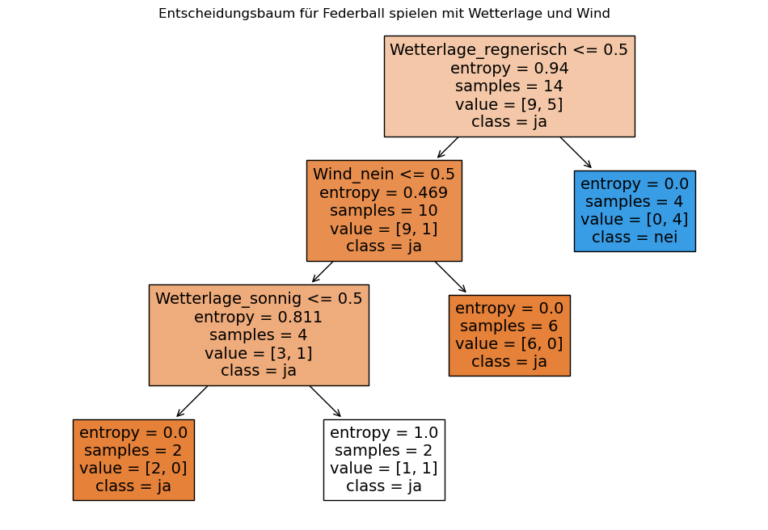
Schritt-für-Schritt Vorgehen beim ID3-Algorithmus
- Berechne die Entropie des gesamten Datensatzes:
Die Entropie des gesamten Datensatzes mit 9 “Ja”- und 5 “Nein”-Einträgen beträgt:
Entropie=0.940, wie oben berechnet.
Dies zeigt die Unreinheit des gesamten Datensatzes – je höher der Wert, desto gemischter ist die Verteilung der Klassen. - Berechne den Informationsgewinn für jedes Attribut:
Der Informationsgewinn für das Attribut “Wetterlage” ist deutlich höher als für das Attribut “Wind”:
Informationsgewinn für “Wetterlage”: 0.682
Informationsgewinn für “Wind”: 0.048Das bedeutet, dass “Wetterlage” der bessere Split für den ersten Entscheidungsbaumknoten ist.
- Wähle das Attribut mit dem höchsten Informationsgewinn:
Basierend auf dem höchsten Informationsgewinn erfolgt der erste Split nach dem Attribut “Wetterlage”.
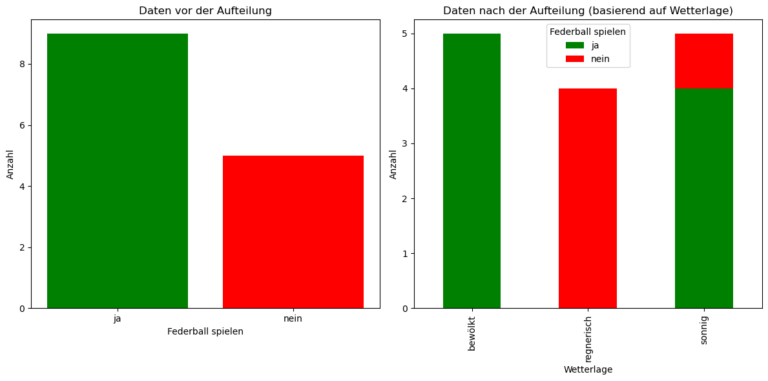
Die drei Untergruppen basierend auf der “Wetterlage” sind:
Sonnig: 5 Datenpunkte (4 “Ja”, 1 “Nein”)
Bewölkt: 5 Datenpunkte (alle “Ja”)
Regnerisch: 4 Datenpunkte (alle “Nein”)
Siehe den Plot unten für eine Visualisierung dieser rekursiven Datenaufteilung. - Wiederhole den Vorgang rekursiv für jede Teilmenge:
Wende denselben Prozess auf jede der Teilmengen an, bis der Baum vollständig gewachsen ist.
Zusammenfassung
Der ID3-Algorithmus ist ein grundlegender Ansatz zur Erstellung von Entscheidungsbäumen, der auf Entropie und Informationsgewinn basiert. Durch die Verwendung dieser Konzepte ist es möglich, Daten effektiv zu klassifizieren und eine verständliche Entscheidungsstruktur zu generieren. Dieser Algorithmus legt den Grundstein für viele erweiterte Techniken im Machine Learning, und durch seine klare mathematische Grundlage ist er leicht nachvollziehbar.
